
The hold-out method for training the machine learning models is a technique that involves splitting the data into different sets: one set for training, and other sets for validation and testing. The hold-out method is used to check how well a machine learning model will perform on the new data. In this post, you will learn about the hold-out method used during the process of training the machine learning model. Do check out my post on what is machine learning? concepts & examples for a detailed understanding of different aspects related to the basics of machine learning. Also, check out a related post on what is data science?
When evaluating machine learning (ML) models, the question that arises is whether the model is the best model available from the model’s hypothesis space in terms of generalization error on the unseen / future data set. Whether the model is trained and tested using the most appropriate method. Out of available models, which model to select? These questions are taken care of using what is called as a hold-out method.
Instead of using an entire dataset for training, different sets called validation set and test set are separated or set aside (and, thus, hold-out name) from the entire dataset and the model is trained only on what is termed as the training dataset.
Table of Contents
The hold-out method for training a machine learning model is the process of splitting the data into different splits and using one split for training the model and other splits for validating and testing the models. The hold-out method is used for both model evaluation and model selection. The following represents the data splits used in hold out method.

When the entire data is used for training the model using different algorithms, the problem of evaluating the models and selecting the most optimal model remains. The primary task is to find out which model out of all models has the lowest generalization error. In other words, which model makes a better prediction on future or unseen datasets than all other models. This is where the need to have some mechanism arises wherein the model is trained on one data set, and, validated and tested on another dataset. This is where the hold-out method comes into the picture.
The hold-out method for model evaluation represents the mechanism of splitting the dataset into training and test datasets. The model is trained on the training set and then tested on the testing set to get the most optimal model. This approach is often used when the data set is small and there is not enough data to split into three sets (training, validation, and testing). This approach has the advantage of being simple to implement, but it can be sensitive to how the data is divided into two sets. If the split is not random, then the results may be biased. Overall, the hold out method for model evaluation is a good starting point for training machine learning models, but it should be used with caution. The following represents the hold-out method for model evaluation.
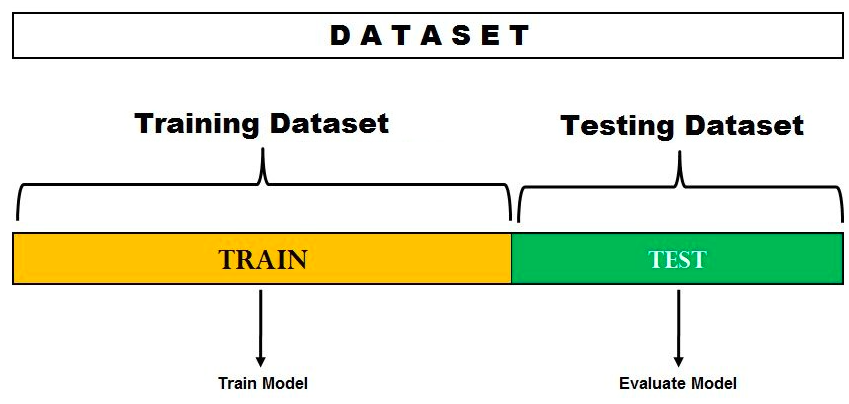
In the above diagram, you may note that the data set is split into two parts. One split is set aside or held out for training the model. Another set is set aside or held out for testing or evaluating the model. The split percentage is decided based on the volume of the data available for training purposes. Generally, 70-30% split is used for splitting the dataset where 70% of the dataset is used for training and 30% dataset is used for testing the model.
This technique is well suited if the goal is to compare the models based on the model accuracy on the test dataset and select the best model. However, there is always a possibility that trying to use this technique can result in the model fitting well to the test dataset. In other words, the models are trained to improve model accuracy on the test dataset assuming that the test dataset represents the population. The test error, thus, becomes an optimistically biased estimation of generalization error. However, that is not desired. The final model fails to generalize well to the unseen or future dataset as it is trained to fit well (or overfit) concerning the test data.
The following is the process of using the hold-out method for model evaluation:
Note that this process is used for model evaluation based on splitting the dataset into training and test datasets and using a fixed set of hyperparameters. There is another technique of splitting the data into three sets and using these three sets for model selection or hyperparameters tuning. We will look at that technique in the next section.
The following Python code showcases how to use the hold-out method for evaluating the performance of a machine learning model by splitting the data into training and test datasets. In this example, the well-known Iris dataset is employed. The code begins by loading the Iris dataset using the load_iris() function from the sklearn.datasets module. Subsequently, the data is divided into training and test sets using train_test_split() from sklearn.model_selection, with a test dataset size of 30% and a fixed random state for reproducibility. A logistic regression model is then initialized, trained on the training dataset, and utilized to make predictions on the test dataset.
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # Load the Iris dataset iris = load_iris() X = iris.data y = iris.target # Split the data into training and test datasets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42) # Initialize and train the model model = LogisticRegression() model.fit(X_train, y_train) # Make predictions on the test dataset y_pred = model.predict(X_test) # Evaluate the model performance accuracy = accuracy_score(y_test, y_pred) print(f"Accuracy: ")
The hold-out method can also be used for model selection or hyperparameters tuning. As a matter of fact, at times, the model selection process is referred to as hyper-parameters tuning. In the hold-out method for model selection, the dataset is split into three different sets – training, validation, and test dataset. When using the hold out method by splitting data into three different sets, it is important to ensure that the training, validation and test datasets are representative of the entire dataset. Otherwise, the model may perform poorly on unseen data.
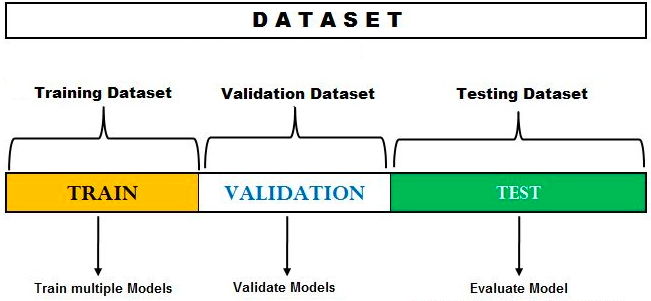
The following process represents the hold-out method for model selection:
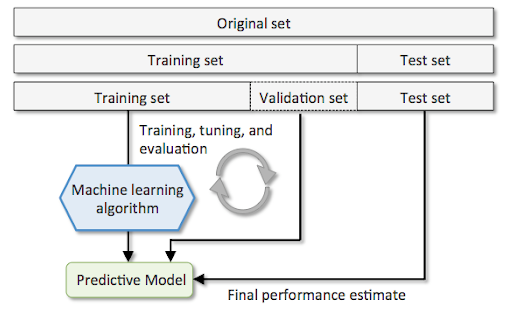
The above can be understood using the following diagram. Note the three different splits of the original dataset. The process of training, tuning, and evaluation is repeated multiple times, and the most optimal model is selected. The final model is evaluated on the test dataset.
The following Python code exemplifies the use of the hold-out method for model selection by dividing the data into training, validation, and test datasets, utilizing the renowned Iris dataset. The code begins by loading the Iris dataset through the load_iris() function from sklearn.datasets. Subsequently, the data is split into training, validation, and test datasets using the train_test_split() function from sklearn.model_selection. The test dataset accounts for 20% of the data, while the training dataset is further divided into training and validation subsets using a 75%/25% split. A logistic regression model is then initialized, trained on the training dataset, and employed to make predictions on the validation dataset.
from sklearn.datasets import load_iris from sklearn.model_selection import train_test_split from sklearn.linear_model import LogisticRegression from sklearn.metrics import accuracy_score # Load the Iris dataset iris = load_iris() X = iris.data y = iris.target # Split the data into training, validation, and test datasets X_train_val, X_test, y_train_val, y_test = train_test_split(X, y, test_size=0.2, random_state=42) X_train, X_val, y_train, y_val = train_test_split(X_train_val, y_train_val, test_size=0.25, random_state=42) # Initialize and train the model model = LogisticRegression() model.fit(X_train, y_train) # Make predictions on the validation dataset y_pred = model.predict(X_val) # Evaluate the model performance on the validation dataset accuracy = accuracy_score(y_val, y_pred) print(f"Validation Accuracy: ") # Make predictions on the test dataset y_pred_test = model.predict(X_test) # Evaluate the model performance on the test dataset accuracy_test = accuracy_score(y_test, y_pred_test) print(f"Test Accuracy: ")
Based on the fundamental techniques discussed in the previous section, there are different types of hold-out methods that are used to improve the machine learning model accuracy by avoiding overfitting or underfitting of the model. The following is the list of some of them:
Hold-out methods are machine learning techniques that can be used to avoid overfitting or underfitting machine learning models. The cross-validation hold out method is one of the most popular utilized types, where a machine learning model will first train using a portion of data, and then it will be tested on what’s left. Leave-one-out cross-validation is another technique that helps avoid these pitfalls by leaving one observation as a test case while training with the rest of the data. If you would like to learn more, please send your queries.
I have been recently working in the area of Data analytics including Data Science and Machine Learning / Deep Learning. I am also passionate about different technologies including programming languages such as Java/JEE, Javascript, Python, R, Julia, etc, and technologies such as Blockchain, mobile computing, cloud-native technologies, application security, cloud computing platforms, big data, etc. I would love to connect with you on Linkedin.
Check out my latest book titled as First Principles Thinking: Building winning products using first principles thinking.